고정 헤더 영역
상세 컨텐츠
본문
지난 포스팅에서는 CoNg 모델이 실제로 형태소 분석을 비롯한 모호성 해소, 문장 분리 등의 과제에서 높은 성능을 보이며 Kiwi에 들어갈 차세대 언어 모델로서의 자격이 충분히 있다는 것을 확인했습니다. 이제 남은 것은 코드를 실제로 짜서 CoNg 모델이 Kiwi 안에서 빠르고 정확하게 잘 돌아가도록 만들기만 하면 됩니다.(참 쉽죠?) 근데 제일 처음 신경망 모델을 도입하기로 결심했을때 설정했던 조건이 있었습니다. 그래서 사실 그냥 잘 돌아가는게 아니라 아래의 두 조건을 만족시키면서 돌아가야합니다.
- 모델 크기는 100MB이내.
- 속도는 현재 KnLM 기반의 분석기와 유사할 것. 혹시나 느려지더라도 1.5배 이상 느려지면 안됨.
둘다 최적화와 관련된 문제가 되겠네요. 전자는 크기 최적화, 후자는 속도 최적화입니다. 둘을 동시에 해결하려면 머리가 아프니 저는 실제 개발 시에는 일단 각개격파로 먼저 속도 최적화를 수행하고 그 이후 모델의 용량을 줄이는 방식으로 접근했는데요, 이번 포스팅에서도 그때와 마찬가지의 순서로 설명을 진행하도록 하겠습니다.
Kiwi CoNg 포스팅 시리즈
- 형태소 분석기 Kiwi CoNg (1/4): 신경망 모델 도입기
- 형태소 분석기 Kiwi CoNg (2/4): CoNg 모델 소개
- 형태소 분석기 Kiwi CoNg (3/4): 모델 성능 비교
- 형태소 분석기 Kiwi CoNg (4/4): 모델 최적화
속도 최적화

속도 최적화는 모델이 동일한 결과를 내도록 정확도는 유지하면서 연산 시간을 최대한 줄이는 것을 말합니다. 속도는 아주 빠르게 만들었으나 모델의 정확도가 팍 떨어져버린다면 아무 의미가 없습니다. 따라서 각 최적화 단계별로 속도가 빨라지면서 정확도가 동일하게 유지된다는 것을 확인하는게 필요한데, 이 포스팅에서는 여백이 부족하여 정확도는 함께 기재하지 못했음을 미리 알리는 바입니다. (마지막 단계인 dimension 축소를 제외하고는 모두 정확도 손실이 없는 최적화였습니다~) 일단 결과부터 보겠습니다.
| 문장당 평균 처리 시간(ms) | 모델 메모리 사용량(MB) | 문장당 평균 처리 시간(ms) | 모델 메모리 사용량(MB) | |
|---|---|---|---|---|
| KnLM | SBG | |||
| 베이스라인 | 0.92 | 368.7 | 2.30 | 377.9 |
| CoNg | CoNg Global | |||
| 최초 구현 | 64.13 | 926.1 | 114.910 | 1058.0 |
| + Batch화 | 13.21 | 926.1 | 31.10 | 1058.0 |
| + 불필요한 탐색 제거 | 3.49 | 926.1 | 19.50 | 1058.0 |
| + 8bit 양자화 | 1.65 | 420.2 | 3.50 | 443.9 |
| + GEMM 커널 최적화 | 0.89 | 420.2 | 1.92 | 443.9 |
| + 탐색 결과 캐싱 | 0.80 | 420.2 | 1.81 | 443.9 |
| + Search SIMD 최적화 | 0.70 | 420.2 | 1.74 | 443.9 |
| + dimension 축소 | 0.58 | 336.9 | 1.58 | 357.1 |
왼쪽에는 Local 모델인 CoNg(및 베이스라인인 KnLM)의 결과가, 오른쪽에는 Global 모델인 CoNg Global(및 베이스라인인 SBG)의 결과가 표기되어 있습니다. Local 모델 기준으로 최초 구현체는 베이스라인보다 60배 이상 느린 상황이었는데요, 다양한 최적화를 통해 최종적으로는 문장당 평균 0.58ms로 베이스라인인 0.92ms보다 50%이상 더 빨라지게 되었습니다. Global 모델에서도 마찬가지로 SBG보다 더 빨라지는 데에 성공했구요. 각 단계에 대해 차근차근 설명해보도록 하겠습니다.
Kiwi가 언어 모델을 사용하는 방법
각 최적화 단계를 설명하기에 앞서 먼저 Kiwi가 언어 모델을 사용하여 어떤 식으로 문장을 형태소로 분석하는지 간단하게 살펴보겠습니다. Kiwi의 형태소 분석은 크게 2단계로 진행됩니다. 먼저 입력된 텍스트에서 가능한 형태소들을 최대한 발견하여 그래프로 변환하는 단계가 있고, 이렇게 변환된 그래프를 탐색하면서 가장 적합한 형태소 배열을 찾는 단계가 있습니다. 두 번째 단계에서 적합한 형태소 배열을 찾기 위해서 언어 모델을 사용하는 것이구요.
말로만 설명하면 감이 잘 안 잡히니 예시를 들면서 소개해보겠습니다. 형태소 분석하면 늘 떠오르는 그 문장~ 바로 "아버지가방에들어가신다."를 생각해볼까요? 첫번째 단계는 이 텍스트에서 가능한 형태소들을 발견하는 것입니다. 앞부분부터 찾아보면 "아버지", "가방", "가", "방", "에" 등이 있을텐데요, 일단은 어떤게 맞는지는 고민하지 않고 최대한 나열하는게 첫번째 단계의 역할입니다. 이렇게 나열한 형태소들을 잘 연결하면 아래와 같이 그래프 구조를 만들 수 있습니다.

여백이 부족한 관계로 "아버지가방에"까지만 표현해봤습니다. 이 그래프는 항상 <BOS>에서 시작하여 <EOS>로 끝나는 방향성 그래프입니다. 즉 BOS에서부터 시작하여 여러 갈림길 중 하나를 선택하면서 나아가다보면 항상 EOS를 만날 수 있게 됩니다. 그리고 각 노드(주황색 동그라미)에는 해당 형태에 대응되는 형태소 목록이 나열되어 있습니다. 1번 아버지의 경우에는 아버지/NNG 하나 밖에 없지만, 2번 가 같은 경우는 가/VV, 가/JKS, 가/NNG 처럼 여러 형태소가 나열되어 있는 경우도 있죠. 이제 BOS 노드에서 시작해서 노드를 하나씩 건너가면서 해당 노드에 포함된 형태소 1개를 고르고 또 다음 노드로 건너가는 그런 상황을 생각해봅시다. 이건 주어진 입력 문장에서 가능한 모든 형태소 조합을 따져보는것과 동일합니다. 예를 들어 0번 노드에서 시작해 5번까지 가능 경우를 생각해보면
- 0 → 1 → 2 → 4 → 5
- 0 → 1 → 3 → 5
노드로는 위와 같이 2가지 경로가 있을 것이고, 각 경로에서 선택할 수 있는 형태소의 조합도 따져보자면
- 0(1가지) → 1(1가지) → 2(3가지) → 4(3가지) → 5(2가지): 1×1×3×3×2 = 18
- 0(1가지) → 1(1가지) → 3(1가지) → 5(2가지): 1×1×2 = 2
첫번째 경로에서는 18가지, 두번째 경로에서는 2가지가 나와서 총 20가지의 형태소 조합이 가능하다는 걸 알 수 있습니다. 이 20가지 중에서 어떤 형태소 조합이 가장 적절한지를 알아야 "아버지가방에"를 바르게 분석할 수 있을텐데요, 이것은 이제 언어 모델이 할 일입니다.

두번째 단계는 위에서 구성한 방향성 그래프의 노드를 전부 순회하면서 최적의 경로를 찾는 것입니다. 최적의 경로를 보관해두기 위해서 Kiwi는 위와 같이 (ID, 부모ID, 형태소, 누적점수)로 구성되는 표를 만들어서 메모를 합니다. 그리고 0번 노드부터 시작하여 언어 모델을 이용해 점수를 계산해나갑니다. (사실 0번 노드는 시작 노드이므로 별도로 계산을 할 필요는 없이 초기화만 해둡니다.) 1번 노드에서는 아버지/NNG라는 형태소가 이전의 결과(ID=0) 다음에 올 로그 확률을 계산합니다. 계산해보니 $-8.5$였는데 그 이전의 결과(ID=0)의 로그 확률 점수가 $0.0$이었으므로 합해서 $-8.5$로 적어둡니다. 1번 노드의 모든 형태소에 대해 계산을 끝냈으니 다음으로 2번 노드로 넘어갑니다. 2번 노드에서도 마찬가지로 이전의 결과(ID=1) 다음에 가/VV, 가/JKS, 가/NNG가 올 확률을 각각 계산합니다. 로그 확률을 계산해보니 $-0.6$, $-1.1$, $-8.7$ 이었고, 이전 결과(ID=1)에 이를 누산하니 $-9.1$, $-9.6$, $-17.2$가 되었습니다. 이와 같이 바로 이전의 결과에 가능한 다음의 결과를 모두 나열하여 언어 모델로 확률 점수를 계산하고 이를 누적해 나가는 것을 반복하다 보면 최적의 경로를 찾을 수 있습니다.
5번 노드까지 탐색했을때의 결과를 보면 ID=17이 $-16.9$으로 가장 점수가 높네요. 이게 최적의 분석 결과라는 건데요, 실제로 이게 어떤 형태소로 구성되어있는지 알고 싶다면 부모ID를 따라서 거슬러 올라가보면 됩니다. 부모 ID를 따라 거슬러 올라가면서 어떤 형태소들이 들어있는지 나열해보면 아래와 같습니다.
- ID=17, 에/JKB
- ID=9, 방/NNG
- ID=3, 가/JKS
- ID=1, 아버지/NNG
- ID=0, <BOS> (끝)
이 결과를 역으로 다시 쓰면 <BOS>, 아버지/NNG, 가/JKS, 방/NNG, 에/JKB 가 됩니다. 다행히도 아버지께서 가방에 들어가시는 참사가 발생하지는 않았군요! 근데 사실 이 탐색 방법을 그대로 쓰긴 어렵습니다. 지금은 문장이 짧아서 노드 개수가 적었고, 각 노드에 들어있는 형태소 목록도 1~3개 정도였으니 망정이지 만약 노드가 수백개가 되고, 각 노드의 형태소 목록도 10개 가까이 된다고 하면 노드를 탐색해나갈때마다 메모하는 표의 크기가 매번 10배가까이 늘어날 것이기 때문입니다. 메모리가 터져나가겠죠? 그래서 탐색 후보를 줄이는 몇 가지 트릭을 사용합니다.
위의 그림에서 5번 노드의 표를 보면 부모ID가 5, 9, 10, 11인 경우만 있고 나머지(6,7,8,12,13,14)는 없습니다. 우리가 알고 싶은 것은 점수가 가장 높은 경로 1가지이므로 사실 1등의 가망성이 없는 경로는 가능하면 미리 쳐내는게 효율적입니다. 그런데 부모가 지금 부진하다고 해서 그 후손들까지 반드시 부진한게 아니라 역전이 충분히 일어날 수 있다는 게 문제를 어렵게 합니다. 그래서 언어 모델이 이전의 n(예시에서는 1)개 형태소만 고려한다는 가정을 도입합니다.
그러면 이전 형태소가동일한 경우 후손들의 언어 모델 점수도 동일해지므로 우리는 이전 형태소가 동일한 것들중 가장 점수가 높은 것만 남기고 나머지는 미리 버릴 수 있습니다. 그래서 4번 노드에서는 ID=9,10,11만 선택하고 나머지는 다음 후손으로 연결되지 않게 미리 잘라낸 것이죠. 이런 과정을 통해 각 표에 저장되는 메모의 크기는 줄이면서 최적의 경로를 탐색하는게 가능해집니다.
CoNg: 최초 구현체
CoNg 모델 구조에 관한 포스팅에서 설명했듯 CoNg은 이전의 n-gram 문맥을 하나의 임베딩 벡터로 만들고, 다음에 나타날 형태소 1개를 임베딩 벡터로 만들어서 둘을 내적한 값을 이용해 확률을 계산합니다. 원래는 이 내적값들에 Softmax를 취해서 확률을 구해야하지만, 앞에서 설명한 것처럼 미리 분모항을 계산하여 저장해두는 트릭을 통해 우리는 임베딩 벡터 한 쌍끼리 내적을 구하기만 해도 Softmax의 연산결과를 알아낼 수 있습니다. 초기 구현체는 이 방식을 따라 충실하게 동작하도록 만들었고, 각 임베딩들은 전부 FP32로 저장했습니다. 벡터 간 내적에는 Eigen 라이브러리를 사용했구요. 그 결과는 제일 위에서 본것처럼 60배 가까이 처참하게 느렸습니다.
Batch화 적용, 불필요한 탐색 제거
| 문장당 평균 처리 시간(ms) | 모델 메모리 사용량(MB) | 문장당 평균 처리 시간(ms) | 모델 메모리 사용량(MB) | |
|---|---|---|---|---|
| CoNg | CoNg Global | |||
| 최초 구현 | 64.13 | 926.1 | 114.910 | 1058.0 |
| + Batch화 | 13.21 | 926.1 | 31.10 | 1058.0 |
| + 불필요한 탐색 제거 | 3.49 | 926.1 | 19.50 | 1058.0 |
가장 먼저 수행한 최적화는 언어 모델 계산의 Batch화입니다. 그림2에서 ID=9, 10, 11 뒤에 에/JKB가 올 확률과 에/IC가 올 확률을 계산하려면 총 6가지 조합에 대한 내적을 구해야합니다. 임베딩의 크기를 4라고 가정하면 아래와 같이 4차원 벡터 간의 내적을 총 6번 계산해야하는 것입니다.

그러나 내적을 구하기 전에 ID=9, 10, 11의 문맥 임베딩을 가져와서 세로로 연결하여 행렬로 만들고, 또 에/JKB와 에/IC에 해당하는 임베딩을 가져와서 가로로 연결하여 행렬을 만들면, 내적연산을 따로 수행하는 대신 아래 그림처럼 두 행렬의 곱셈을 계산하는 방식으로 6가지 조합의 계산 결과를 한번에 얻을 수 있습니다.

근데 사실 위처럼 내적을 따로 6번 계산하는거나 아래처럼 행렬 곱셈 1번을 하는 것이나 최종적인 연산량은 동일합니다. 오히려 행렬을 구성하는 단계에서 추가적인 오버헤드가 발생하므로 더 비효율적인것 아닐까요? 다행히도 그렇지 않습니다! 아래와 같이 행렬로 구성하여 한번에 곱셈을 수행하는 것이 캐시 메모리 재사용 때문에 더 빠릅니다. 사실 위의 내적에서 병목이 되는 부분은 곱셈 연산 그 자체가 아니라 문맥에 해당하는 임베딩과 형태소에 해당하는 임베딩을 RAM에서 읽어오는 부분이기 때문입니다.
그래서 추가적인 전처리를 수행하더라도 연산 자체를 한번에 모아서 하게 되면, 임베딩을 메모리로부터 읽어오는 작업은 1번만 하면 되고, 그 이후에는 캐시에 올라간 메모리를 재사용할 수 있어서 속도가 훨씬 빨라지게 됩니다. 이렇게 언어 모델 계산을 Batch화 하는 작업을 통해서 3~5배 정도 소요 시간을 줄일 수 있었습니다.
8bit 양자화, 최적화된 GEMM 커널 구현
위에서 설명했다시피 주요 병목은 RAM에 흩어져 있는 임베딩을 로드하는 작업입니다. 이 작업은 임베딩의 메모리 상 크기에 비례해서 시간이 걸리므로 메모리 상 크기를 줄일 수 있다면 속도를 높일 수 있습니다. 일반적으로 실수를 저장하는데에 FP32(C언어의 float 타입, 32비트 단정밀도 부동소수점)를 사용하는데 사실 아주 정밀한 연산 결과가 필요한게 아닌 이상 신경망 모델에서 굳이 FP32를 쓰지 않아도 동일한 결과를 얻을 수 있다는게 널리 알려져 있습니다. 그래서 자주 사용하는 기법이 양자화(Quantization)입니다. 양자화의 사전적인 의미는 연속인 값을 불연속적인 값으로 바꾸는 것을 이야기하지만 신경망에서 쓰일때는 흔히 32비트 실수를 더 적은 비트로 나타내는 작업을 가리킵니다.
| 문장당 평균 처리 시간(ms) | 모델 메모리 사용량(MB) | 문장당 평균 처리 시간(ms) | 모델 메모리 사용량(MB) | |
|---|---|---|---|---|
| CoNg | CoNg Global | |||
| + 불필요한 탐색 제거 | 3.49 | 926.1 | 19.50 | 1058.0 |
| + 8bit 양자화 | 1.65 | 420.2 | 3.50 | 443.9 |
| + GEMM 커널 최적화 | 0.89 | 420.2 | 1.92 | 443.9 |
예를 들어 FP32를 Int8(8bit 정수)로 양자화하면 표현 가능한 값은 덜 촘촘해지지만 메모리 사용량이 1/4이 되어서 속도 향상을 기대할수 있는 것이죠. 뿐만 아니라 Int8 양자화는 가장 널리 쓰이는 일반적인 양자화 기법이기 때문에 최신 CPU에서는 Int8로 양자화된 신경망을 처리할 때 사용할 수 있는 가속 명령어들을 갖추고 있습니다. 따라서 Int8로 양자화를 수행할 경우, 메모리 병목이 1/4로 줄어들고 추가로 연산 속도 역시 최신 CPU에서 이론상 최대 4배까지 빨라질 수 있습니다.
단점은 정밀도가 낮아져서 모델의 정확도가 낮아질수 있다는 것인데요, 이는 여러 겹의 레이어로 구성된 모델에서 레이어마다 오차가 전파되면서 누적되는 상황에서 문제가 되지 CoNg처럼 단일 레이어로 구성된 모델에서는 사실 전혀 문제가 되지 않습니다. 즉, CoNg 입장에서 Int8 양자화는 단점은 없고 장점만 있는 최적화 기법이니 고민할 필요 없이 도입하는게 맞습니다. 실제로 베이스라인 Int8 GEMM 커널에서도 속도가 2배 이상 크게 개선된 것을 확인할 수 있었습니다.
Int8 양자화의 가능성을 보았으니 이제 커널 최적화를 진행해서 속도를 극한으로 쥐어짜내는 작업을 해야합니다. 바퀴를 다시 발명하지 말라는 격언처럼, 굳이 직접 최적화를 하기보다는 이미 잘 최적화된 Int8 GEMM (qgemm) 커널을 그대로 가져와서 사용하는 것도 나쁘지 않은 선택입니다. 그러나 몇 가지 프로파일링을 해본 결과 현재 오픈소스로 공개된 qgemm 커널들이 CoNg의 상황에서 최적으로 동작하지 않는다는 걸 발견했습니다. 원인은 크게 메모리 병목과 SIMD 연산 상에서의 병목이었습니다.
메모리 병목은 CoNg에서는 Matrix A를 구성하기 위해서 흩어져있는 문맥 임베딩에서 우리가 원하는 값들만 선택해서 모으는 작업(Gather)을 먼저 수행해야한다는 점 때문에 발생했습니다. Gather연산은 Batch화 과정에서 피할수 없기 때문에 무조건 메모리 복사 연산이 1회는 일어나야할 것으로 보입니다. 문제는 GEMM Kernel 내부에서도 실은 Matrix A를 다시 Sub block로 쪼개어 복사하는 과정이 있기 때문에 CoNg 시나리오에서는 임베딩 값을 총 2회 복사하게 됩니다. GEMM Kernel 내부에서는 왜 굳이 Matrix A를 Sub block로 쪼개어 복사할까요? 일일히 설명하기에는 좀 복잡하므로 링크로 대체하고 요점만 적어보자면 Cache 활용을 최대한 높여서 메모리에 직접 접근하는 연산 횟수를 줄이기 위해서입니다.
이를 위해서 보통 L1 Cache에 들어갈 수 있는만큼 Matrix A의 일부 Block을 Cache용 메모리 공간에 복사하는 작업을 GEMM Kernel에서 수행합니다. 그럼 어차피 GEMM Kernel 내부에서 Matrix A를 복사해서 Cache용 공간에 넣을거라면 애초에 Gather를 하지 않고 바로 Embeddings에서 원하는 Index만 선택해서 Cache용 메모리 공간에 직접 복사하도록 하면 Gather 연산을 생략할 수 있지 않을까요? 맞습니다! 그래서 Gather + GEMM Kernel을 한번에 수행하기 위해 직접 intrinsic function(어셈블리 명령어와 1대1 대응되는 함수)들을 활용해 Kernel을 작성했습니다.
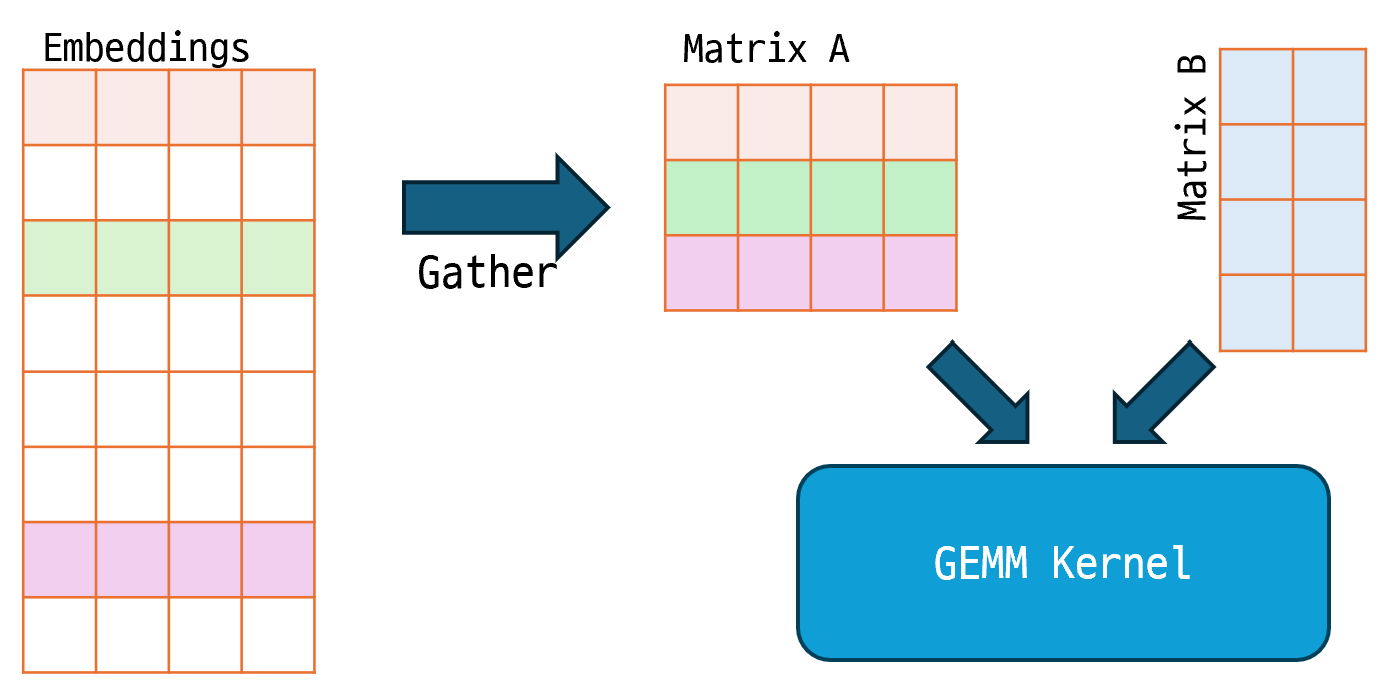

그리고 SIMD 연산 상의 병목도 있었는데요, GEMM 커널은 (m, n) 행렬과 (n, k) 행렬을 곱한 결과인 (m, n) 행렬을 구하는게 목적인데 여기서 보통 m, n, k의 크기가 충분히 크고 비슷한 경우에 최고의 효율을 내도록 최적화됩니다. m, n이 너무 작거나 k가 큰 경우에는 Matrix를 Sub block으로 나눠도 재사용할만한 경우가 많이 나오지 않기 때문이죠. 그래서 m, n이 작거나 k가 너무 큰 경우에는 보통 내적 연산을 수행하는 함수로 분기해서 처리하는게 일반적입니다.
그럼 실제로 CoNg 모델에서 사용하는 GEMM 연산의 입력은 어떤 크기일까요? k는 임베딩의 크기이므로 적당히 큰 256~384 정도가 되지만, m, n는 통계를 내보니 아래와 같이 주로 m=1~16, n=1~4인 경우가 대부분이었고 그보다 더 큰 Matrix 입력은 거의 없는 것을 확인할 수 있었습니다. 따라서 기존 커널과는 다르게 아주 작은 크기의 m, n에 대해 GEMM 커널을 최적화하는게 필요했습니다.

먼저 가장 많이 쓰이는 n=1, 2, 3, 4에 대해서 AVX512 VNNI instruction을 이용해 전용 커널을 구현했고(2.93 -> 2.49ms), 커널에 Loop Unrolling, Thread-Local Storage를 공유하는 최적화를 적용(2.49 -> 1.92 ms)했습니다. n > 4에 대해서는 n=1~4 커널을 여러 번 수행하는 것으로 대체했습니다. (이게 최적은 아니겠지만 자주 사용되지 않는 입력에 대해 일일히 최적화하기에는 개발자의 시간도 소중하니깐요~)
탐색 결과 캐싱, Search SIMD 최적화

여기까지 오니 이제 GEMM 연산이 전체 실행시간에서 차지하는 비율이 약 22% 밖에 되지 않게 되었습니다. 오히려 나머지 부분에서 시간을 더 쓰고 있는 건데요, 나머지 부분에서 가장 병목이었던 구간은 1) 문맥 임베딩의 ID를 찾기 위해 Trie를 탐색하는 부분과 2) 현재 노드까지의 중간 결과에서 이전 문맥 ID가 동일한 사례들을 찾기 위해 해시맵에 값을 넣고 찾는 부분이었습니다. 전자는 Trie 탐색이라는 특성상 메모리 접근 지점이 매번 바뀌는게, 후자는 C++ 표준 라이브러리의 std::unordered_map 특성 상 해시에 저장되는 값들이 불연속적으로 위치하여 메모리 접근 지점이 불연속적인게 L1 Cache 적중률을 낮춰서 병목을 일으키고 있었습니다.
| 문장당 평균 처리 시간(ms) | 모델 메모리 사용량(MB) | 문장당 평균 처리 시간(ms) | 모델 메모리 사용량(MB) | |
|---|---|---|---|---|
| CoNg | CoNg Global | |||
| + GEMM 커널 최적화 | 0.89 | 420.2 | 1.92 | 443.9 |
| + 탐색 결과 캐싱 | 0.80 | 420.2 | 1.81 | 443.9 |
| + Search SIMD 최적화 | 0.70 | 420.2 | 1.74 | 443.9 |
먼저 문맥 Trie 탐색은 뭘해도 불규칙한 메모리 접근 패턴을 보일 수 밖에 없는데요, 다행히도 동일한 노드 내에서는 대체로 문맥이 유사하기 때문에 비슷한 Trie 경로를 따라가는 경우가 많았습니다. 이를 이용해 최근에 탐색한 Trie 노드의 결과를 캐싱해두고 다음에 동일한 경로를 탈 경우 캐시를 사용하도록 수정하여 병목을 줄일 수 있었습니다.
그리고 해시맵 최적화는 아예 해시맵을 포기하는 것으로 달성했습니다. 해시맵이 점근적으로는 임의의 key에 대해 O(1) 접근 시간을 보장하는 반면 선형 탐색은 임의의 key를 찾기 위해 O(n)이 소요됩니다. 그렇지만 형태소 분석 경로를 탐색할때 컨테이너의 크기는 주로 몇 십 정도의 크기이므로 사실 O(1)이냐 O(n)이냐는 속도에 큰 영향을 주지 않고 오히려 캐시 적중률이 속도에 더 큰 영향을 미칩니다. 또 해시맵은 key가 연속된 위치에 배치되지 않으므로 SIMD 연산으로 한번에 n개의 값을 비교할 수 없는 반면, 선형 탐색은 key가 연속되어 배치되므로 SIMD로 가속이 가능합니다.
이런 점들을 모두 종합한 결과 해시맵을 버리고 선형 탐색 기반의 dictionary 자료 구조를 구현했습니다. 해시 크기는 1바이트로 줄이고 이를 연속된 배열에 배치해놓아 AVX512에서는 한번에 64개의 값(AVX2에서는 32개의 값)을 조회할 수 있게 만들었습니다. 프로파일링 결과 컨테이너의 크기가 64개를 넘어가는 경우가 거의 없었으므로 사실상 메모리 로드 1번, 비교 1번을 통해 원하는 hash가 컨테이너에 없다는 걸 알아낼수 있고, 동일한 hash가 존재하는 경우에만 key를 비교하여 그 값을 찾아낼수 있었습니다.
앞만 보고 달리다가 문득 뒤를 돌아서 Kiwi CoNg과 베이스라인를 비교해보니, 벌써 Local 모델에서는 KnLM(0.92ms)보다 CoNg이 0.70ms로 더 빨라졌고, 마찬가지로 Global 모델에서도 SBG(2.30ms)보다 CoNg Global이 1.74ms로 더 빨라졌습니다. 신경망 모델이라서 많이 느려지지 않을까 걱정했는데, 당초 예상을 뛰어 넘어서 속도 향상을 달성했네요! 이제 남은건 모델 크기입니다.
크기 최적화
| 모델 크기 (MB) | ZIP 압축 후 모델 크기 (MB) | 형태소 분석 정확도 (F1) | 모호성 해소 정확도 (%) | 문장 분리 정확도 (Norm F1) | |
|---|---|---|---|---|---|
| 베이스라인(SBG) | 37.84 | 28.30 | 81.787 | 64.025 | 81.77 |
| CoNg Global 8bit 양자화 | 111.43 | 105.83 | 81.536 | 87.500 | 83.76 |
| 7bit | 111.43 | 94.62 | 81.625 | 87.812 | 84.01 |
| 6bit | 111.43 | 84.50 | 81.525 | 87.468 | 83.76 |
| 5bit | 111.43 | 75.46 | 81.602 | 87.737 | 84.11 |
| 4bit | 111.43 | 61.62 | 81.236 | 86.102 | 83.26 |
| Packed 4bit Group=8 | 74.56 | 70.52 | 81.432 | 87.340 | 84.25 |
| Sparsity=50% | 111.43 | 77.32 | 81.610 | 87.468 | 84.11 |
| Packed 4bit Group=8, Sparsity=50% | 74.56 | 66.96 | 81.450 | 87.145 | 83.24 |
| Packed 4bit Sparsity=50% Block=4 | 86.85 | 63.76 | 81.414 | 86.235 | 83.60 |
| Packed 4bit Sparsity=50% Block=8 | 74.56 | 52.91 | 81.144 | 86.838 | 84.22 |
앞서 양자화에서 설명한 것처럼 Int8 양자화는 사실상 양자화의 표준과도 같습니다. 그래서 8bit를 베이스라인으로 잡고 모델 크기와 성능을 비교해나가기 시작했습니다. 참고로 CPU에서 가속이 지원되는 데이터 타입은 Int8까지이므로 8bit 보다 적은 비트로 양자화하는 것은 모델의 크기를 줄일수 있어도 속도를 올릴 순 없습니다. 임베딩이 lower-bit 타입으로 저장되어있다 할지라도 어차피 다시 8bit로 변환한 다음 연산에 투입되어야하니깐요. 그래서 4~7bit는 모델을 저장할때도 아예 8bit를 유지하면서 저장하도록 했습니다. (그래서 모델 크기도 모두 111.43MB로 동일합니다.)
5bit까지는 bit수가 줄어들어도 전반적으로 모델이 성능이 유지되는걸 볼 수 있는데요, 4bit부터는 정확도가 급락하는게 보이기 시작합니다. 현실적으로 사용 가능한 최소 정밀도는 5bit정도라고 볼 수 있겠습니다. 단순히 정밀도를 줄이는 대신 Packed 4bit라는 방식도 고안하여 시도해봤습니다. 8개의 Weight를 1개의 Group으로 묶어서 해당 Group에 Local Zeropoint와 Local Scale을 도입하는 방식입니다. 각 Weight는 4비트로 표현되므로 0~15 사이의 값을 가질 수 있고, Local Zeropoint는 2비트로 6, 7, 8, 9 중 하나의 값을 갖습니다. 그리고 Local Scale은 6비트로 9~72의 값을 갖습니다. 이 때 실제 Weight가 가리키는 값은 다음과 같이 계산됩니다:
$$R = (W - Z) \times S / 9 $$
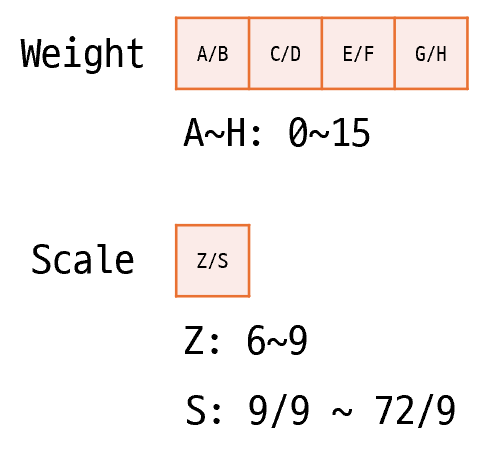
8개마다 Local Zeropoint와 Local Scale이 추가되므로 더 높은 다이내믹을 표현할 수 있게 되어 4bit로 인한 정밀도 손실을 보완해줍니다. 물론 8개의 가중치를 결국 5바이트로 표현하는 것이므로 실제 저장공간은 비압축시 5bit와 동일하게 사용하게 됩니다. 대신 압축한 경우에는 5bit보다 모델 크기가 더 많이 줄어들고 또 모델의 성능 역시 5~6bit 사이 정도가 되어 나쁘지 않은 절충안인 것으로 확인되었습니다.
양자화 말고도 모델 크기를 줄이는데에 자주 쓰이는 방법으로 희소화(Sparsification)가 있습니다. 희소화는 가중치 행렬에서 0인 부분의 비율을 늘리는 것이라고 정의할 수 있으며, 이때 0인 값의 비율을 희소성(Sparsity)라고 합니다. 당연히 희소성이 높아질수록 대부분의 값이 0이 되므로 압축 효율이 좋아지는 대신 모델이 더 많은 정보를 잃어버리게 됩니다. 그리고 희소화 역시 8bit 미만의 양자화처럼 CPU에서 직접 가속 연산을 지원하지 않기 때문에 속도 향상에는 도움이 거의 안되고 일반적으로 모델 크기를 줄이는 용도로 자주 쓰입니다. 희소화의 효과에 대해서도 실험해본 결과 Sparsity=50%인 경우 압축후 모델 크기는 5~6bit 사이로 나왔으며 성능도 역시 그 정도로 나왔습니다.
양자화와 희소화는 서로 별개의 경량화 기법이므로 둘을 동시에 적용하는 것도 가능합니다. 실제로 Packed 4bit 양자화와 Sparsity=50%를 동시에 적용한 경우 압축 후 모델크기가 67MB까지 내려갔음에도 성능은 4bit보다 높은 것을 확인할 수 있었습니다. 이 정도면 성능 손실도 감내할만하고 모델 크기도 충분히 합리적인 것 같습니다.
만약 압축률을 더 높이고 싶다면 희소화시 구조적 희소화(Structured Sparsification)를 적용할 수도 있습니다. 구조적 희소화는 0이 아무 위치에나 등장하는 것이 아니라 블럭 단위로 연속해서 나타나도록 강제하는 것입니다. 당연히 연속해서 0이 나타나므로 압축 시 효율이 더 높아집니다. 위의 표에서 Block=4, Block=8가 적힌 부분이 구조적 희소화를 적용한 것이구요, 실제로 성능은 좀 더 낮아지지만 모델 크기는 최대 53MB까지 압축되는 것을 볼 수 있습니다. 고무적인 건 이렇게까지 압축하더라도 기존 베이스라인인 SBG모델보다는 높은 성능을 유지한다는 점입니다~
다양하게 양자화와 희소화 실험을 해본 결과, 성능 손실과 압축 크기의 균형점에 위치한 Packed 4bit Group=8 + Sparsity=50%이 배포용으로 가장 적합하다고 판단되어 이를 최종 모델로 선정했습니다. 이로써 처음 설정했던 두 가지 기준을 모두 만족하는 CoNg 모델을 완성했습니다!!!
최종 결과
다음은 한국어 위키백과에서 1000개 문서를 임의로 뽑아 형태소 분석을 실시했을때의 초당 분석 속도(KB/s)를 측정한 결과입니다. 모든 경우에서 CoNg > KnLM, 그리고 CoNg Global > SBG인 양상을 보여주고 있습니다.
| 장비 | 아키텍처 | KnLM | SBG | CoNg | CoNg Global | CoNg Global 메모리 사용량 |
|---|---|---|---|---|---|---|
| Ryzen 9700X | AVX512-VNNI | 195.72 | 82.14 | 243.12 | 124.13 | 357.1MB |
| AVX2 | 193.44 | 80.48 | 240.88 | 117.78 | 357.1MB | |
| SSE4.1 | 181.26 | 77.72 | 237.69 | 107.08 | 357.1MB | |
| SSE2* | 187.27 | 68.86 | 201.76 | 75.69 | 646.1MB | |
| Apple M2 | ARM Neon* | 200.31 | 55.53 | 228.78 | 83.03 | 646.1MB |
AVX512 VNNI 명령어까지 최대한 활용해서 최적화한 덕분에 최신 CPU에서 가장 빠르게 동작합니다. 참고로 SSE2는 너무 오래전 명령어셋이라서 양자화 가속이 지원되지 않는 문제로 FP32로 처리되고, Apple M시리즈는 AMX(행렬 곱셈 가속 연산 명령어)가 내장되어 있는데 자기네들만 사용하려고 숨겨놓은게 괘씸해서(사실은 쓰고 싶어도 어떻게 써야하는지 잘 몰라서) 최적화 커널을 작성하지 못했습니다. FP32로 폴백하여 동작해도 메모리 사용량이 좀 늘어날뿐 속도가 크게 느려지는 것은 아니라서 구형 CPU나 ARM 등 다른 아키텍처에서도 무리 없이 사용할 수 있어보입니다!
끝이 아니라 새로운 시작!
지금까지 총 4회에 걸쳐 Kiwi CoNg 모델의 도입 이유와 구조, 성능, 최적화에 대해서 소개해드렸습니다. 오래 전부터 구상해오던 모델을 마침내 성공적으로 구현해내서 무거운 짐을 내려놓은 기분인데요, 사실 CoNg의 구현 완료는 끝이 아니라 새로운 시작이라고 할 수 있습니다. 제일 첫 포스팅에서 언급했듯이 신경망 모델을 도입한 것은 학습 데이터가 부족한 상황에서도 더 높은 일반화 성능을 얻기 위함입니다. 즉 다시 말하면 이제 데이터 부족으로 시도해보지 못했던 다양한 분야에 대해서 Kiwi가 도전할 수 있게 되었다는 것입니다.
예를 들자면 사투리라든지 전근대 한국어처럼 표준어와 약간 유사하지만 알고보면 꽤 다른 언어들에 대한 분석, 혹은 단어 의미 중의성 해소와 같은 더 세밀한 변별이 필요한 분석 등 흥미롭지만 쉽지 않은 과제들이 기다리고 있습니다. 물론 CoNg 모델만으로는 역부족일 수도 있습니다만, 적어도 기존의 통계 기반 모델보다는 훨씬 잘할 것이라는 건 확실하겠죠?
앞으로도 더욱 발전할 한국어 형태소 분석기 Kiwi에 많은 관심가져주시길 바라면서 이번 Kiwi CoNg 포스팅 시리즈는 여기에서 마무리하도록 하겠습니다. 감사합니다~!
'프로그래밍 > NLP' 카테고리의 다른 글
| 형태소 분석기 Kiwi CoNg (3/4): 모델 성능 비교 (0) | 2025.05.19 |
|---|---|
| 형태소 분석기 Kiwi CoNg (2/4): CoNg 모델 소개 (1) | 2025.05.11 |
| 형태소 분석기 Kiwi CoNg (1/4): 신경망 모델 도입기 (0) | 2025.05.04 |
| 한국어 말뭉치를 통한 사이시옷 사용 실태 조사 (1) | 2024.11.04 |
| LLM으로 게임 텍스트 번역해보기 (2) | 2024.08.31 |
| 형태소 분석기의 모호성 해소 성능을 평가해보자 (4) | 2022.03.27 |


댓글 영역